| 离散数学 | 您所在的位置:网站首页 › equivalent fraction数学含义 › 离散数学 |
离散数学
|
文章目录
第三章 关系3.1.1.本章概述
3.2.关系3.2.1关系的概念3.3.2.关系的性质3.3.3.关系的组成与复合3.2.4.关系的表示
3.3.闭包(Closure)3.3.1.闭包的定义
3.4.等价(Equivalence)3.4.1.等价关系(Equivalence Relations)3.4.2.等价类3.4.3.划分
3.5.偏序(Partial order)3.5.1.偏序关系与偏序集3.5.2.一些经典的偏序关系3.5.2.1.字典序(Lexicographic Order)3.5.2.2.拓扑排序(Topological Order)
3.5.3.哈斯图(Hasse Diagrams)3.5.4.偏序集中的元素3.5.5.格
第三章 关系
3.1.1.本章概述
关系的定义、关系的五大性质、关系的组成和复合、关系的矩阵表示、关系图表示; 三种闭包; 等价关系、等价类、划分 偏序、字典序、哈斯图、偏序集中的特殊元素 3.2.关系 3.2.1关系的概念定义: 集合A到B的二元关系R为 A × B A\times B A×B的子集,用于刻画A中的元素和B中的元素的对应关系。 关系实质上是序偶 (x,y)的集合,其中序偶的第一个元素来自集合A,第二个元素来自集合B。 关系与集合、函数的联系 关系本质是集合,是序偶的集合。 函数是特殊的关系,或者说关系使我们所熟悉的函数的拓展。因为函数要求 定义域domain里面的每一个元素都有与之对应的元素并且不可有多个对应,但关系不要求。
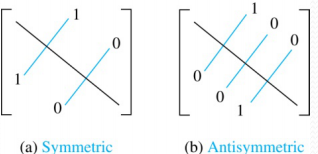
显然,由定义可知,一个不是自反的关系,不一定就是反自反的。 对称性(symmetric) 定义: 设 R R R 为定义在集合 X X X 上的二元关系,如果对于每个 x , y ∈ X x,y\in X x,y∈X ,每当 x R y xRy xRy ,就有 y R x yRx yRx ,则称集合 X X X 上关系 R R R 是对称的。 ∀ x ∀ y [ ( x , y ) ∈ R → ( y , x ) ∈ R ] \forall x \forall y[(x,y)\in R \rightarrow (y,x)\in R] ∀x∀y[(x,y)∈R→(y,x)∈R]反对称性(antisymmetric) 定义: 设 R R R 为定义在集合 X X X 上的二元关系,如果对于每个 x , y ∈ X x,y\in X x,y∈X ,每当 x R y xRy xRy 和 y R x yRx yRx 必有 x = y x=y x=y ,则称 R R R 在 X X X 上是反对称的。 ∀ x ∀ y [ ( x , y ) ∈ R ∧ ( y , x ) ∈ R → x = y ] \forall x \forall y[(x,y)\in R \wedge (y,x)\in R \rightarrow x=y ] ∀x∀y[(x,y)∈R∧(y,x)∈R→x=y]对称与反对称的概念不是对立的,一个关系可能同时具有也可能都不具有这两种性质。 同时不具有的例子有很多,而同时具有的例子呢? 形如: R = { < a , b > ∣ a = = b , a ∈ A , b ∈ A } 或 者 R = ∅ R = \{|a==b ,a\in A,b\in A\} 或者R = \empty R={∣a==b,a∈A,b∈A}或者R=∅,即可同时满足对称性与反对称性。 传递性(transitive) 定义: 设 R R R 为定义在集合 X X X 上的二元关系,如果对于每个 x , y , z ∈ R x,y,z\in R x,y,z∈R ,每当 x R y , y R z xRy,yRz xRy,yRz ,就有 x R z xRz xRz ,则称集合 X X X 上关系 R R R 是传递的。 ∀ x ∀ y ∀ z [ ( x , y ) ∈ R ∧ ( y , z ) ∈ R → ( x , z ) ∈ R ] \forall x \forall y \forall z [(x,y)\in R \wedge (y,z)\in R \rightarrow (x,z)\in R] ∀x∀y∀z[(x,y)∈R∧(y,z)∈R→(x,z)∈R] 3.3.3.关系的组成与复合关系的组成(combination) 关系的本质是集合,故而集合的一系列运算,关系也都可以进行。 设 R 1 , R 2 R_1,R_2 R1,R2为两个关系,譬如,可进行下列运算。 R 1 ∪ R 2 R_1 \cup R_2 R1∪R2 R 1 ∩ R 2 R_1 \cap R_2 R1∩R2 R 1 − R 2 R_1 - R_2 R1−R2 等等。 关系的复合(composition) 设 R R R 为 X X X 到 Y Y Y 的关系, S S S 为从 Y Y Y 到 Z Z Z 的关系,则 S ∘ R S \circ R S∘R 称为 R R R 和 S S S 的复合关系,表示为 X X X到 Z Z Z的关系。 可以用两重循环去求得。 关系自身的复合 关系 R R R 本身所组成的复合关系可以写成: R ∘ R , R ∘ R ∘ R , ⋯ , R ∘ R ∘ ⋯ ∘ R ⏞ n R \circ R,R \circ R \circ R,\cdots,\overbrace{R \circ R \circ \cdots \circ R}^n R∘R,R∘R∘R,⋯,R∘R∘⋯∘R n ,分别记作 R 2 , R 3 , ⋯ , R n R^{2},R^{3},\cdots,R^{n} R2,R3,⋯,Rn ,一般地, R n = R n − 1 ∘ R R^{n}=R^{n-1}\circ R Rn=Rn−1∘R 。 一个重要定理 传递关系的幂必是关系的子集。 i.e. A A A上的关系 R R R具有传递性,当且仅当 R n ⊆ R R^n\subseteq R Rn⊆R(n=1,2,3……), 此定理可以用数学归纳法证明。 充分性 取 n = 2 , R 2 ⊆ R n =2,R^2\subseteq R n=2,R2⊆R,根据关系幂的定义, ∀ x ∀ y ∀ z , x R y , y R z \forall x \forall y \forall z,xRy,yRz ∀x∀y∀z,xRy,yRz有 ( x , z ) ∈ R ∘ R , i , e , ( x , z ) ∈ R 2 (x,z) \in R\circ R,i,e,(x,z)\in R^2 (x,z)∈R∘R,i,e,(x,z)∈R2,又 R 2 ⊆ R R^2\subseteq R R2⊆R,所以 ( x , z ) ∈ R (x,z)\in R (x,z)∈R必要性 利用数学归纳法,显然 n = 1 n=1 n=1时结论成立,假设 R n ⊆ R R^n\subseteq R Rn⊆R,往证 R n + 1 ⊆ R R^{n+1}\subseteq R Rn+1⊆R, 根据 R n + 1 = R n ∘ R R^{n+1}=R^n\circ R Rn+1=Rn∘R的定义, ∀ ( x , z ) ∈ R n + 1 \forall (x,z)\in R^{n+1} ∀(x,z)∈Rn+1,必 ∃ y ∈ A \exists y\in A ∃y∈A,使得 ( x , y ) ∈ R n , ( y , z ) ∈ R (x,y)\in R^{n},(y,z)\in R (x,y)∈Rn,(y,z)∈R,又 R n ⊆ R R^n\subseteq R Rn⊆R,所以, ( x , y ) ∈ R (x,y)\in R (x,y)∈R。 根据R具有传递性的定义,如果 ( x , y ) ∈ R , ( y , z ) ∈ R , (x,y)\in R,(y,z)\in R, (x,y)∈R,(y,z)∈R,,则有 ( x , z ) ∈ R (x,z)\in R (x,z)∈R。 所以, ∀ ( x , z ) ∈ R n + 1 \forall (x,z)\in R^{n+1} ∀(x,z)∈Rn+1,有 ( x , z ) ∈ R (x,z)\in R (x,z)∈R,根据子集的定义, R n + 1 ⊆ R R^{n+1}\subseteq R Rn+1⊆R。 3.2.4.关系的表示用矩阵表示关系 m i j = { 1 , i f ( a i , b j ) ∈ R 0 , i f ( a i , b j ) ∉ R m_{ij}=\begin{cases}1,if(a_i,b_j)\in R\\0,if(a_i,b_j)\notin R\end{cases} mij={1,if(ai,bj)∈R0,if(ai,bj)∈/R 表示在一个集合上的关系是一个方阵。 如果关系具有自反性,那么主对角线上的元素都为1; 其他地方不受限定。 如果关系具有对称性, ∀ i , j a i , j = a j . i \forall i,j \ \ a_{i,j}=a_{j.i} ∀i,j ai,j=aj.i 或者说, M R = M R T M_R=M^{T}_R MR=MRT 如果关系具有反对称性,
∀
,
i
,
j
a
i
,
j
=
1
−
a
j
,
i
\forall ,i,j \ \ a_{i,j}=1-a_{j,i}
∀,i,j ai,j=1−aj,i 下面是对称性和反对称性的特征矩阵 关系的运算用集合表示 用有向图表示关系 集合中的每个元素都用一个点表示,每个有序对表示成一条带有箭头的弧表示。 关系的性质与图的特征 自反性:所有顶点都有自环(loop) 反自反性: 图中没有自环出现。 对称性:图中没有单向边。 反对称性:图中无双向边 传递性: x − > y , y − > z x->y,y->z x−>y,y−>z,则必有 x − > z x->z x−>z,直观上来看形成了一个三角形。 3.3.闭包(Closure) 3.3.1.闭包的定义定义 3 - 8.1 设 R R R 是 X X X 上的二元关系,如果有另一个关系 R ′ R' R′ 满足: R ′ R' R′ 是自反的(对称的,可传递的)。 R ′ ⊇ R R' \supseteq R R′⊇R 。对于任何自反的(对称的,可传递的)关系 R ′ ′ R'' R′′ ,如果有 R ′ ′ ⊇ R R'' \supseteq R R′′⊇R ,就有 R ′ ′ ⊇ R ′ R'' \supseteq R' R′′⊇R′ 。则称关系 R ′ R' R′ 为 R R R 的自反(对称、传递)闭包。记作 r ( R ) r(R) r(R) ( s ( R ) s(R) s(R) , t ( R ) t(R) t(R) )。更一般地来说,设 R R R是集合 A A A上的关系,如果存在包含R的具有性质P的关系S,并且S是所有包含R且具有性质P的子集,那么S称为R关于性质P的闭包。 注意:一个关系关于某种性质的闭包不一定存在。 在这个定义里,除了关系 R R R,和闭包 R ′ R^{'} R′,还引入了关系 R ′ ′ R^{''} R′′,就是为了强调从关系R转换为满足某种性质的关系时,需要尽可能添加尽可能少的序偶。这就保证闭包的产生是唯一。 (这里的三个字母分别是 reverse、symmetric 和 transmit 的首字母) 自反闭包 R ′ = R ∪ △ , △ = { ( a , a ) ∣ a ∣ ∈ A } R'=R\cup \triangle,\triangle = \{(a,a)|a|\in A \} R′=R∪△,△={(a,a)∣a∣∈A},其中 △ \triangle △称为对角关系。对称闭包 R ′ = R ∪ R − 1 , R − 1 = { ( b , a ) ∣ ( a , b ) ∈ R } R'=R\cup R^{-1},R^{-1}=\{(b,a) |(a,b)\in R \} R′=R∪R−1,R−1={(b,a)∣(a,b)∈R}传递闭包 传递闭包的求法相对复杂,具体可看这篇文章。 3.4.等价(Equivalence) 3.4.1.等价关系(Equivalence Relations)定义:如果一个关系是自反的、对称的、传递的,那么这个关系就称为等价关系。 元素的等价 如果两个元素由于等价关系而相关联,则称它们是等价的,记为 a a a~ b b b。 模m同余关系 定义关系 R = { ( a , b ) ∣ a ≡ b ( m o d m ) } R=\{(a,b)|a\equiv b(mod \,\ m)\} R={(a,b)∣a≡b(mod m)},模m同余关系就是一种等价关系。 注意: a ≡ b ( m o d m ) ≡ m ∣ ( a − b ) a\equiv b(mod \,\ m) \,\ \equiv m|(a-b) a≡b(mod m) ≡m∣(a−b) 3.4.2.等价类 定义: 设 R R R 为定义在集合 A A A 上的等价关系,对任何 a ∈ A a \in A a∈A ,集合 [ a ] R = { x ∣ ( a , x ) ∈ R } [a]_R = \{ x \vert (a,x)\in R \} [a]R={x∣(a,x)∈R} 称为元素 a a a 形成的 R R R 等价类。以模m同余关系为例,它定义在整数集合 Z Z Z上,模m同余关系的等价类叫做模m同余类。具体地, [ 0 ] m = { … … , − 2 m , − m , 0 , m , 2 m , … … , } [0]_m =\{……,-2m,-m,0,m,2m,……,\} [0]m={……,−2m,−m,0,m,2m,……,}, [ 1 ] m = { … … , − 2 m + 1 , − m + 1 , 1 , m + 1 , 2 m + 1 , … … , } [1]_m =\{……,-2m+1,-m+1,1,m+1,2m+1,……,\} [1]m={……,−2m+1,−m+1,1,m+1,2m+1,……,} …… [ m − 1 ] m = { … … , − m − 1 , − 1 , m − 1 , 2 m − 1 } [m-1]_m=\{……,-m-1,-1,m-1,2m-1\} [m−1]m={……,−m−1,−1,m−1,2m−1} 注: Z m = { [ 0 ] , [ 1 ] , [ 2 ] , … … , [ m − 1 ] } Z_m=\{[0],[1],[2],……,[m-1]\} Zm={[0],[1],[2],……,[m−1]}称为模m剩余类的集合。 3.4.3.划分A A A中两个元素的等价类或者相等或者不相交,换言之,两个元素等价类不可能出现只有部分元素相同的情况。 三个等价命题 (i) a R b aRb aRb (ii) [ a ] = [ b ] [a]=[b] [a]=[b] (iii) [ a ] ∩ [ b ] ≠ ∅ [a]\cap [b]\ne\varnothing [a]∩[b]=∅这里只给出简易证明。 往证 ( i ) (i) (i)和 ( i i ) (ii) (ii)等价,通过证明互为子集。 往证 ( i i ) (ii) (ii)和 ( i i i ) (iii) (iii)等价,显然。 往证 ( i i i ) (iii) (iii)和 ( i ) (i) (i)等价,假定交集中的某一个元素为 c c c,然后根据等价类的定义和等价关系的对称性、传递性可证得结论。 划分的定义 集合S的划分是其不相交子集的集合,并且这些不相交子集的并集就是S 令
S
S
S 为给定非空集合,
A
=
{
A
1
,
A
2
,
⋯
,
A
m
}
A=\{A_1,A_2,\cdots,A_m\}
A={A1,A2,⋯,Am} ,其中
A
i
⊆
S
,
A
i
≠
∅
(
i
=
1
,
2
,
⋯
,
m
)
A_i\subseteq S,A_i\ne\varnothing(i=1,2,\cdots,m)
Ai⊆S,Ai=∅(i=1,2,⋯,m) 且
⋃
i
=
1
m
A
i
=
S
\bigcup\limits_{i=1}^mA_i=S
i=1⋃mAi=S ,集合
A
A
A 称作集合
S
S
S 的覆盖。如果除以上条件外,还另有
A
i
∩
A
j
=
∅
(
i
≠
j
)
A_i\cap A_j=\varnothing(i\ne j)
Ai∩Aj=∅(i=j) ,则称
A
A
A 是
S
S
S 的划分。 由定义知,所谓划分就是一个集合,它里面的元素是由等价关系确定的等价类。 自然,这些元素的交集必为空。 商集 集合 S S S 上的等价关系 R R R ,其等价类集合 { [ a ] R ∣ a ∈ S } \{ [a]_R \vert a \in S \} {[a]R∣a∈S} 称作 S S S 关于 R R R 的商集,记作 S / R S/R S/R 。 划分与等价关系的联系 (i) 集合 S S S 上的等价关系 R R R ,决定了 S S S 的一个划分,该划分就是商集 S / R S/R S/R 。 (ii)集合 S S S 的一个划分确定 S S S 的元素间的一个等价关系。 3.5.偏序(Partial order) 3.5.1.偏序关系与偏序集定义 设 A A A 是一个集合,如果 A A A 上的一个关系 R R R ,满足自反性,反对称性和传递性,则称 R R R 是 A A A 上的一个偏序(关系),并把R记为“ ≼ \preccurlyeq ≼ ”。 ( A , ≼ ) (A,\preccurlyeq ) (A,≼) 称作偏序集(poset)。 集合A中的元素称之为偏序集的元素。 可比较性 偏序集中的元素a,b是可比较的,如果 a ≤ b a≤b a≤b或者 b ≤ a b≤a b≤a 。如果a,b是偏序集中的元素,但是即不存在 a ≤ b a≤b a≤b,也不存在 b ≤ a b≤a b≤a,则称a,b是不可比较的。 可比较性反映在关系图中就是单向边的存在与否。 (注:之所以把这样的关系式偏的、部分的,正是因为有些元素的并不具有这样的可比较的关系,即不可比较的)。 全序集(线序集) 如果 ( S , R ) (S,R) (S,R)是偏序集,并且S中每对元素都是可比较的,则称S为全序集或线序集,R为全序或线序。一个全序集,也称之为链。 良序集 对于偏序集 ( S , ≼ ) (S,\preccurlyeq) (S,≼),如果它是一个全序集,并且 S S S的每一个非空子集都有一个最小元素,那么称它为良序集。 3.5.2.一些经典的偏序关系 3.5.2.1.字典序(Lexicographic Order) 定义: 给定两个偏序集 ( A 1 , ≤ 1 ) (A_1,≤_1) (A1,≤1)和 ( A 2 , ≤ 2 ) (A_2,≤_2) (A2,≤2), A 1 × A 2 A_1\times A_2 A1×A2上的字典序定义为, ( a 1 , a 2 ) < ( b 1 , b 2 ) (a_1,a_2) |
【本文地址】


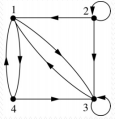 上图表示关系
(
1
,
3
)
,
(
1
,
4
)
,
(
2
,
1
)
,
(
2
,
2
)
,
(
2
,
3
)
,
(
3
,
1
)
,
(
3
,
3
)
,
(
4
,
1
)
,
(
4
,
3
)
{(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)}
(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)
上图表示关系
(
1
,
3
)
,
(
1
,
4
)
,
(
2
,
1
)
,
(
2
,
2
)
,
(
2
,
3
)
,
(
3
,
1
)
,
(
3
,
3
)
,
(
4
,
1
)
,
(
4
,
3
)
{(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)}
(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,3),(4,1),(4,3)